Theoretical framework
Entropy (H(X))
- Definition: A measure of unpredictability or information content.
- Formula:
- Interpretation: The average unpredictability in the outcomes of the random variable X; higher entropy means more unpredictability.
Mutual Information (I(X; Y))
- Definition: A measure of the amount of information that one random variable contains about another random variable.
- Formula:
- Interpretation: The reduction in uncertainty of X due to the knowledge of Y; a mutual information of zero means X and Y are independent.
Relation between Entropy and Mutual Information
-
Mutual Information can also be expressed in terms of entropy:
-
Formula:
-
The diagram below illustrates this relationship:
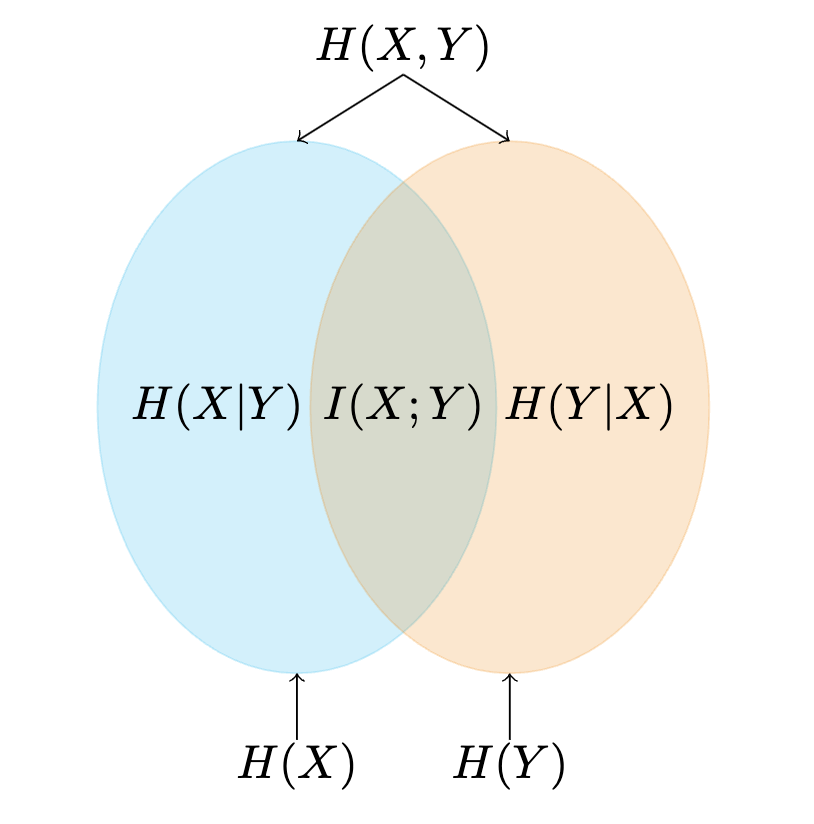
Mutual Information to Entropy
Mutual Information (I(X; Y)) can be expanded to show its relationship with Entropy (H(X)):
-
Initial Expression:
-
Expansion:
-
Simplification:
-
Final Form:
Step-by-Step Explanation
- Start with the definition of mutual information.
- Split the log term into two, using properties of logarithms.
- Recognize the definition of expected value for entropy
- Observe that mutual information is the difference between the entropy of X and the entropy of X given Y.
Implication
- This shows that mutual information is essentially the amount of uncertainty in X that is reduced by knowing Y.
- It quantifies how much knowing one variable informs us about another.
Example Calculation
- Consider a fair die with outcomes 1 through 6, each with an equal probability of
- Entropy
- If we know the outcome of the die is even, mutual information
Channel Capacity
Gaussian channels are a class of channels that are widely used in information theory.
Noise is additive and Gaussian distributed.
Channel capacity can be expressed as the maximum mutual information between the input and output of the channel.
Water Filling Algorithm
The water-filling algorithm is used to find the optimal power allocation for a gaussian channel. It is used to maximize the mutual information between the input and output of the channel.
Water Filling Algorithm
The optimal power allocation is given by the following optimization problem:
-
-
-
-
Water Filling Algorithm
This metaphorical ”water filling” ensures that channels with lower noise levels receive more power because they can transmit information more effectively. Channels with higher noise
levels receive less power, as they contribute less to the overall capacity.
The Channel capacity is the sum of the capacities of each channel.
Calculating Empowerment
Linear Response Approximation
Linear response approximation is a powerful concept used in control theory. It allows us to approximate the dynamics of a system linearly around a set point, typically a null action or equilibrium. This approach not only facilitates the analysis of the exact trajectory but also enables us to understand the influence of small changes in the control signal on the system's evolution.
Fundamental Notation
The state of the system can be expressed as:
Where:
Recursive Mapping and Sensitivity
The recursive mapping from
Sensitivity of
Where
Senstivity is a measure of how much the state of the system changes in response to a change in the control signal.
Applying empowerment to the inverted pendulum
System Dynamics
The dynamics equations for the inverted pendulum can be defined by:
Where:
- \(\theta(t)\) is the angle of the pendulum.
- \(\dot{\theta}(t)\) is the angular velocity of the pendulum.
- \(d(t)\) is the control signal.
- \(g\) is the acceleration due to gravity.
- \(l\) is the length of the pendulum.
- \(m\) is the mass of the pendulum.
- \(W(t)\) is the Wiener process.
Control Strategy
For a duration
Compute channel capacity
The channel capacity is calculated using the following equation:
Where:
(Obtained using SVD decomposition)
(Calculated using the water filling algorithm)
Empowerment-Based Control
We apply an empowerment-based control algorithm to the pendulum, which is given by the following equation:
Conclusion
Conclusion
- Improves decision-making & adaptability
- Contributes to theoretical & practical AI development
- Future Direction: Integration in complex systems (e.g., humanoid robots)
- Proof of Concept: Successful in pendulum control systems
This study highlights the promising path of empowerment for advancing robotics and autonomous systems.